- 2. Pitch shifting
2. Pitch shifting
The first thing to do is to make sure we understand what is pitch shifting. The pitch of a sound corresponds to the set of frequencies the sound is made of. The best way to understand this is to look at a choir. There are both men and women singing but the women will have a higher pitch than the men. What pitch shifting does is it takes the sound produced at a given pitch and changes its frequencies. For instance, by shifting up the pitch of a man who is singing, we could end up with a sound where it sounds like a woman is singing instead.
2.1 Music theory and timbre
The musical range is divided in many octaves. Each octave is made of twelve semitones, also referred to as half steps. Each semitone corresponds to a specific note. A pure note is made of a single sinusoid at the fundamental frequency. The next figure shows you the most common notes with their corresponding fundamental frequency.
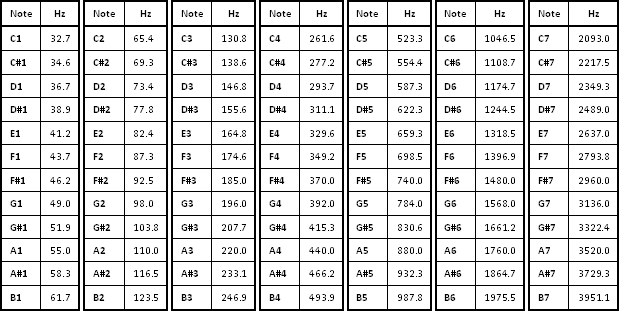
Figure 2.1: Notes and their fundamental frequency
However, the same note played by different instruments does not produce the same sound. This is because each note is usually made of a fundamental frequency but also a set of harmonics. Harmonics components have a frequency that is an integer number times the fundamental frequency. The organization of the harmonics with respect to each other allows one to recognize the instrument being played. This is the musical instrument signature, more specifically referred to as the timbre.
The next figures shows how the note A4 (A on the 4th octave) is represented as a pure note and as a note played by different instruments. The pure note is made only of the fundamental frequency 440Hz while the note played by instruments is made of many harmonics (2x440=880Hz, 3x440=1320Hz, etc.) You see that the amplitude of the harmonics is different for each instrument, which characterizes their respective timbre.
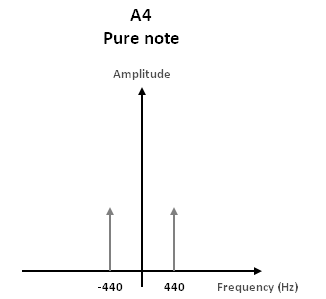
Figure 2.2: Pure note
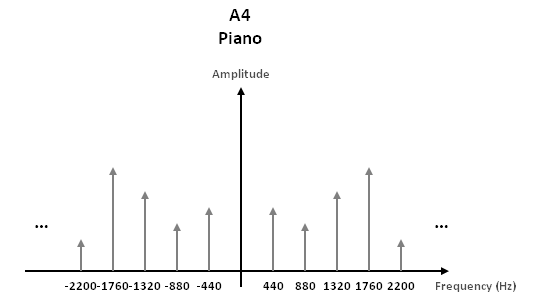
Figure 2.3: Piano note
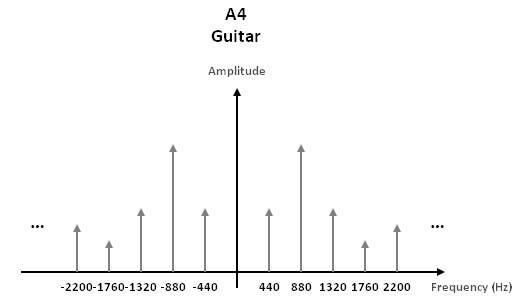
Figure 2.4: Guitar note
2.2 Frequency scaling
As mentioned above, each note corresponds to a fundamental frequency. This frequency is defined in the next equation, where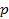 
stands for the number of semitones and 
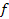for the frequency in Hertz.
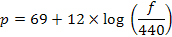
Equation 2.1: Relationship between semitones and fundamental frequency
From a musical point of view, pitch shifting consists of shifting a melody by one or many semitones up or down, as shown in the next equation. The initial semitone index is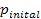 
, the number of semitones for shifting is 
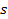and the final semitone index is 
.
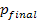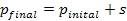
Equation 2.2: Relationship between the initial and final semitone indexes for pitch shifting
From a signal point of view, this consists in scaling the fundamental frequency and the harmonics by a specific factor, shown in equation 2.3. The initial note frequency is 
, the number of semitones for shifting is 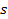and the final note frequency is 
.
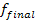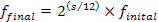
Equation 2.3: Relationship between the initial and final frequencies for pitch shifting
The previous concepts are summarized in figure 2.5. A piano keyboard is used for better visual explanation purposes; however the same theory could be applied to a guitar neck. One octave is selected and each note is identified according to musical conventions (C, C#, D, etc.) There are twelve semitones per octave. This implies that shifting up or down a note by a complete octave is equivalent to scaling the spectrum by two or one half respectively. This figure illustrates the spectrum spreading (with a factor of 2(4/12)) for a pitch shifting of four semitones up (from C to E).
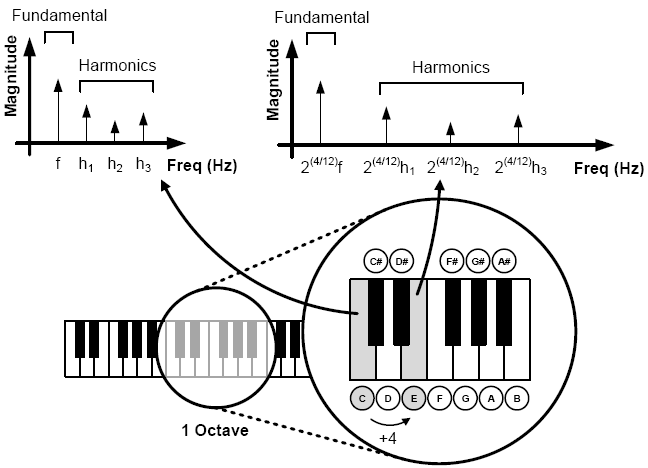
Figure 2.5: Spectrum spreading when pitch shifting by four semitones
2.3 A simple solution... that does not work
So now you might think: what is so hard about pitching shifting anyway? If I record a song and then make it play twice as fast, then all the frequencies will be doubled and the pitch will be shifted up by one octave. You are right, but your signal is now twice shorter!
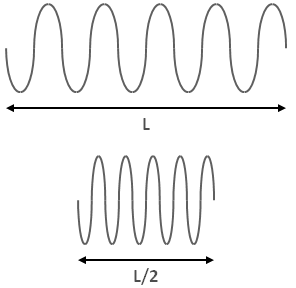
Figure 2.6: Pitch shifting by affecting duration
2.4 The good way to do it
So what if we can first take the song, double the length without affecting the pitch and then play it twice as fast? All frequencies would be doubled and therefore the pitch would be shifted AND the duration would match the initial one.
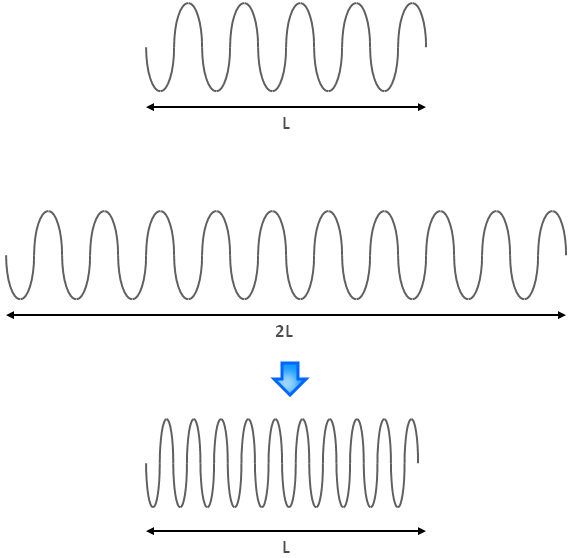
Figure 2.7: Pitch shifting without affecting duration
That would work perfect and our algorithm is based on this principle. The next section explains in detail how the algorithm will work.
|
Previous: Introduction |
Next: Algorithm |
Copyright © 2009- François Grondin. All Rights Reserved.